Hash Map이란 무엇인가?
1. key-value 형태로 데이터를 저장하는 자료구조
2. 하나의 key는 하나의 value 에 맵핑
3. key는 uniqueness를 보장함
그 Key를 해시함수를 통해서 만든다.
hash 함수 결과값은 대부분 정수입니다(인덱싱을 위해 만든 값이니 어찌보면 당연)
=> 만든 이유는 데이터 메모리의 낭비를 줄이기 위해서!
GPT야 도와줘🙋♂️
해시맵은 데이터를 저장하고 검색하는 보다 효율적인 방법을 제공하기 위해 만들어졌습니다. 해시맵을 사용하기 전에는 데이터가 배열이나 목록에 저장되는 경우가 많았기 때문에 특히 데이터 양이 증가함에 따라 특정 데이터 조각을 검색하는 데 시간이 많이 걸렸습니다.
해시맵이 해결할 수 있는 특정 문제 중 하나는 중복 데이터 문제입니다. 예를 들어 각각 고유한 고객 ID를 포함하는 대규모 고객 레코드 데이터 세트를 생각해 보십시오. 특정 고객의 레코드를 검색해야 하는 경우 일치하는 고객 ID가 있는 레코드를 찾을 때까지 전체 데이터 세트를 검색해야 합니다. 이것은 특히 데이터 세트가 매우 큰 경우 시간이 많이 걸리는 프로세스가 될 수 있습니다.
그러나 해시맵을 사용하여 데이터를 저장하면 고유 ID로 특정 고객 레코드를 빠르게 검색할 수 있습니다. 해시맵은 전체 데이터 세트를 검색할 필요 없이 고객 ID를 키로 사용하여 레코드에 직접 액세스합니다.
데이터 검색에 필요한 시간을 줄이는 것 외에도 해시맵은 메모리를 보다 효율적으로 사용할 수 있도록 하여 메모리 낭비를 줄이는 데 도움이 될 수 있습니다. 이는 해시맵이 메모리에서 사용하지 않는 공간을 최소화하는 방식으로 데이터를 저장하기 때문입니다.
with java..
HashMap<String, Integer> map = new HashMap<String, Integer>();
map.put("apple", 1);
map.put("banana", 2);
map.put("orange", 3);
int value = map.get("banana");
System.out.println(value); // Output: 2
with C++..
stl 라이브러리
unordered_map<string, int> my_map = {{"apple", 1}, {"banana", 2}, {"orange", 3}};
int value = my_map["banana"];
cout << value << endl; // Output: 2
with Python..
딕셔너리..
my_dict = {"apple": 1, "banana": 2, "orange": 3}
value = my_dict["banana"]
print(value) # Output: 2
with Dart..
Map..
Map<String, int> myMap = {'apple': 1, 'banana': 2, 'orange': 3};
int value = myMap['banana'];
print(value); // Output:with Javascript..
Object..
let myObj = {'apple': 1, 'banana': 2, 'orange': 3};
let value = myObj['banana'];
console.log(value); //
구현체
* 배열을 사용하여 구현
배열을 통해서 어떻게 구현하는가?
배열은 크기와 상관없이 데이터에 상수시간으로 접근이 가능하다.
Key는 hash를 먼저 구한다. (hash function을 통해서)
array[hf(key) % M] = valueM이 'Index'가 됩니다. 모듈러 연산을 하게 되면 사용하는 값.
=> 모듈러 연산은 나머지 연산인데, 종종 해시 코드를 배열이나 테이블의 인덱스로 변환하는 데 사용됩니다. 해시 코드는 배열/테이블의 크기로 나누어지고 나머지는 인덱스로 사용됩니다. 이는 나머지가 항상 0과 '배열/테이블의 크기 - 1' 사이에 있기 때문에 인덱스가 데이터 구조의 범위 내에 있도록 보장하기 때문입니다.
모듈러 연산을 통해 indexing을 위한 값을 만들어내고, 이것이 상수시간(O(1))로 데이터에 접근할 수 있도록 해준다.
해시 충돌
** 서로 다른 key들이 같은 hash를 가질 때 발생 **
첫번째 조건 : key1 != key. But, hf(key1) == hf(key2)
//조건
key1 != key 이지만
But
hf(key1) == hf(key2) 일 때
두번째 조건: hf(key1) != hf(key2) BUT! hf(key1) % M == hf(key2) % M
Hash는 각기 다르게 나왔으나, indexing을 위한 모듈러 연산을 했을 때의 결과가 같은 경우.
//조건2
hf(key1) != hf(key2)
BUT!
hf(key1) % M == hf(key2) % M이 경우 또한
해시맵 안에서의 해시 충돌이라고 부를 수 있다.
다시 맵핑 시켰을 때 해시 콜리젼이 일어날 수 있지 않을까요?
** Perfect hash Function 구현의 어려움
key1 != key2 && hf(key1)!= hf(key2)
이 조건이 항상 이렇게 보장되는 것이 perfect hash function이라고 하는데
사실상 구현은 불가능하지요.
input은 무한한 String의 조합으로 양이 엄청난데,
output은 항상 정수여야한다. 이게 참 어려운 일이지요.
물론 모듈러 연산으로 되돌리는 경우에도 참 어려운 일이지요.
내 서비스에 가입한 사람의 핸드폰 번호를 key, 그 사람 정보를 value로 hash map에 저장한다면?
일단 실제 서비스들에서 실제 key범위를 모두 예측해서 hash map을 잡지 않는다. 작게 잡지.
실제가 데이터가 들어갈 것 같은 범위 (예시로 1000개라고 하면) 1000개의 value값으로 예상해서 만든다.
절대 hash Map은 key 사이즈로 범위를 잡아 만들지 않는다 -> 이는 심한 메모리 낭비예요.
해시 맵의 해시 충돌 해결 방법
1. Seperate Chaining 해결 방식: 추가적인 공간을 활용하여 해결하는 방식
*링크드 리스트 사용 (자바는 이렇게 하는 것 가틈)
2. Open addressing: 충돌 발생 시 인접한 비어있는 공간(bucket)에 저장
* Linear probing: 고정폭으로 이동하여 빈 공간을 찾음
* Quadratic probing:
* Double Hashing
Separate Chaining
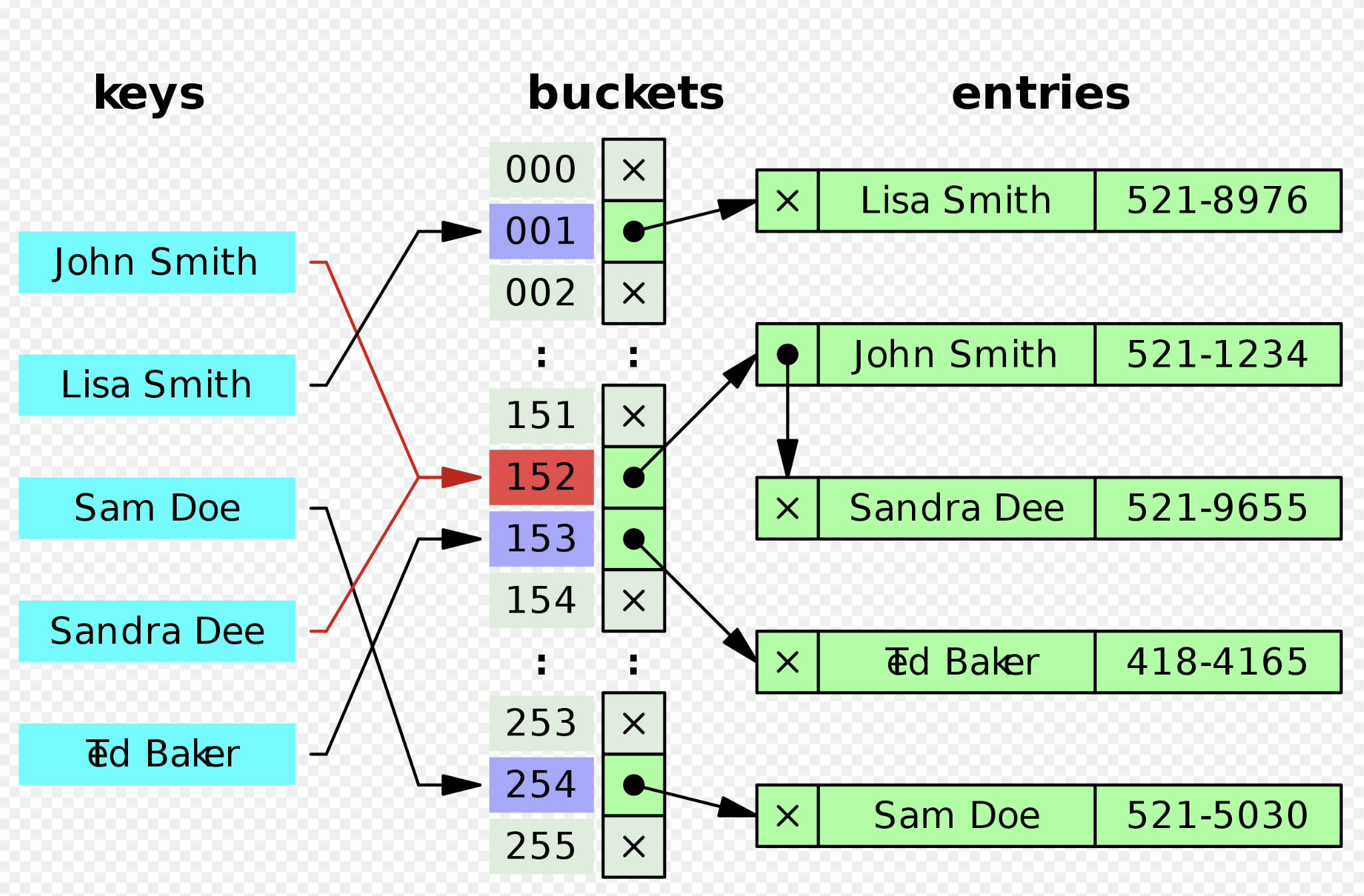
구현 방식
bucket의 index 를 따라 들어가 만난 공간에
원래는 value를 넣어서 저장하는 것이겠으나,
seperate chaining은 여기서 다른 노드를 가리키는 포인터를 저장합니다.
**여기서 재밌는 점: 해시충돌이 여러번 날 때 데이터 노드의 연결
데이터의 노드가 뒤로 줄줄이 이어지는 것이 아닌,
hash map의 헤드(맨 처음 인덱스) 가 원래 가리키고 있던 곳에서
새로운 노드를 추가해서 원래 head가 가리키고 있던 노드를 가리키게하고,
헤드에는 새롭게 추가한 노드의 주소를 가리키게 하여
헤드의 바로뒤에 추가한다.
뒤로 잇는 방식일 때는,
링크드 리스트가 끝없이 길어졌다면 모든 노드를 거쳐
맨 뒤로 가서 추가해야하기 때문에 그렇게 좋은 방식이 아닙니다.
그리하여, head의 바로 뒤에 새로운 노드를 추가하여 잇는 링크드 리스트 방식.
* 단점이라면, 추가적인 메모리 공간을 사용한다는 점
* 또 단점이라면, 링크드 리스트가 길어지면 찾는데 꽤 걸릴 수 있다는 점 ?
Open addressing
: 새로운 공간을 추가하지 않고, 이미 확보한 공간만을 가지고 문제를 해결하는 방식. 인접한 공간에 충돌이 난 데이터를 추가시켜주는 방식입니다.
1. Linear probing
hf_lp(key, i ) = hf(key) + i
i 는 충돌횟수.

데이터들이 좀 Clustering되는 경향이 살짝 있음. 군집현상..근처에 저장되니까
Open addressing: Quadratic probing

hf_qp(key, i) = hf(key) + i**
(예는 제곱이지만, 복잡한 식이 들어갈 수 있음)
i는 여전히 충돌횟수.
linear probing을 사용했을 때 발견된 clustering군집현상이 좀 분산됩니다.
이러면 충돌횟수 및 비교횟수가 확줄어들 수 있겠죠? (해시 충돌이 한 key에서 연속적으로 일어났을때, 공간을 4번 똑똑 두드려볼 것은 2번이면 되게 할 수있음- 대충)
Open addressing: Double Hashing
그런데 이제 i제곱으로 퍼트리는것도 모자라다!
(왜냐면 충돌이 일어난 횟수만큼 확인했던 위치를 또 확인하게 되는 일이 발생하니까)
hash function을 두개 써서 더 겹칠일 없게 하자
=> Double Hashing.
hf_dh(key, i) = hf(key) + i * 2nd_hf(key)
이건 위의 QB 에서 해시값을 처음 구했을떄 그 해시 값이 같으면 결국 수식이 같아
계속해서 따라야 한다는 단점이 있어 그것을 보완한 방식이다.
그런데 DH방식도 재미있는 것은 2nd_hf(key)의 값이 map사이즈와 서로소여야 한다는 점.
****Open addressing 주의점*****


중간 연결고리 역할을 하는 Key의 삭제 시,
이미 있는 값도 없다고 판단할 수 있음
=> 중복된 값이 저장될 수 있음
linear probing을 할 때,
삭제시 DELETE 같은 상징적인 마킹을 해준다!
"여긴 뭔가 있었지만 삭제된 공간이야! 다음 공간을 한 번 볼 필요가 있단다"
라는 뜻의 마킹.
=> 하지만, DELETE를 만나면 항상 다음 값을 확인하게 된다.
다 DELETE가 되어있는 해시맵에서 새롭게 값을 추가한다고 생각해보면,
모든 DELETE를 갔다가 그제서야 처음 값에 저장을 하게 됩니다..!
꽤나 큰 오퍼레이션 비용이 들게될지도?
그래서 데이터들을 한칸씩 땡기는 오퍼레이션을 넣을 수도 있습니다.
))))예시
Java는 어떻게 해시 충돌을 해결했을까?
jdk7 은 seprate chaining을 활용
jdk8은 linkded list와 red black tree를 혼용한 Seperate chaining을 활용한다.